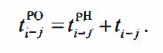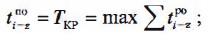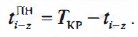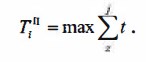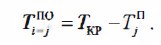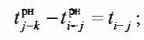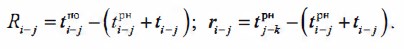18.3 Расчет сетевых графиков
Расчет сетевых графиков сводиться к численному определению его пара-метров. Поэтому сначала перечислим их.
При расчете сетевых графиков определяются следующие параметры:
— ранние начала и окончания работ;
— поздние начала и окончания работ;
— продолжительность критического пути;
— общие и частные резервы работ.
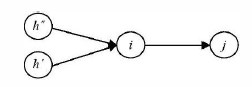
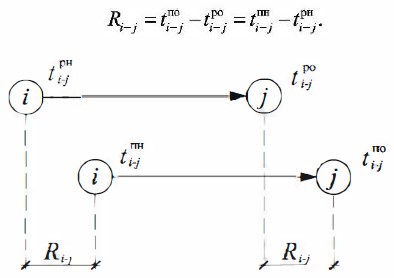
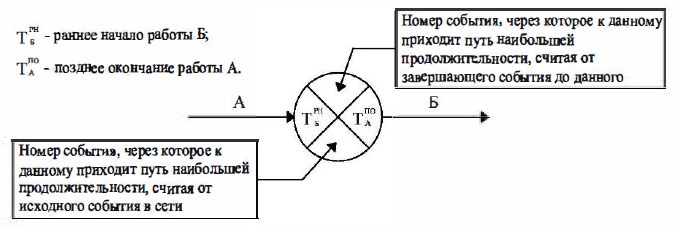
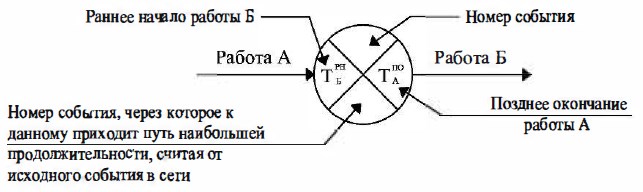
Рис. 18.8 Расчетная модель
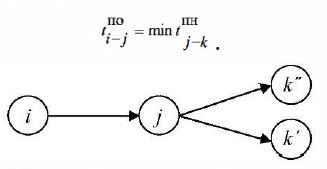
Раннее начало работы (рис. 18.9) равно продолжительности максимального пути от исходного события графика до начального события данной работы:
Рис. 18.9 Модель расчета ранних начал
Для начальных (исходных) работ:
— раннее начало принимается равным 0;
— раннее окончание численно равно продолжительности работы. Максимальное раннее окончание одной из завершающих работ определяет продолжительность критического пути.
Позднее окончание работы определяется разностью между продолжительностью критического пути и продолжительностью максимального пути от конечного события данной работы до завершающего события графика.
Позднее окончание любой работы (рис. 18.1 О) равно наименьшему из поздних начал последующих работ:
Рис. 18.10 Модель расчета поздних окончаний
Позднее начало работы равно разности между величинами ее позднего окончания и продолжительности.
Для завершающих работ сетевого графика:
— позднее окончание равно величине продолжительности критического пути:
= позднее начало завершающей работы равно разности между продолжительностью критического пути и продолжительностью данной работы:
Рис. 18.11 Модель расчета общих резервов
Рис. 18.12 Модель расчета частных резервов
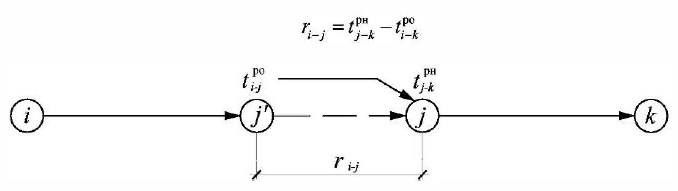
Частный резерв времени отличается от нуля, если в конечное событие работы входят две и более работы.
Методы расчета сетевых графиков
Классическим методом, положившим начало теории расчета сетевых графиков, является табличный метод, или, как говорят, алгоритм расчета сетевого графика по таблице.
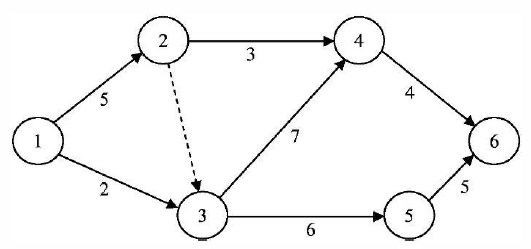
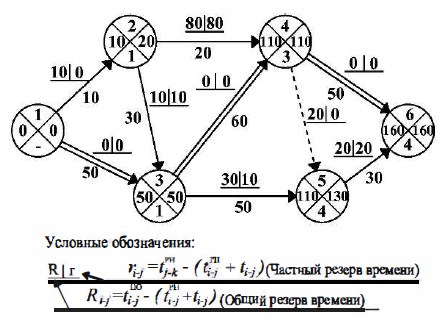
Пример графика для расчета табличным методом приведен на рис. 18.13. В этом случае определение параметров сетевого графика выполняется в таблице.
Рис. 18.13 Пример графика для расчета табличным методом и методом потенциалов
Заполнение таблицы ведется в следующем порядке.
2) Производят расчет ранних параметров работ построчно сверху вниз.
3) Определяют продолжительность критического пути, равная максимальному из ранних окончаний завершающих работ.
4) Рассчитывают поздние параметры работ. Расчет ведется построчно снизу вверх, от завершающих работ до исходных.
5) Определяют общие и частные резервы времени (их можно определить по каждой работе вразбивку).
Определяют перечень работ, составляющих критический путь, т.е. работ, не имеющих резервов времени.
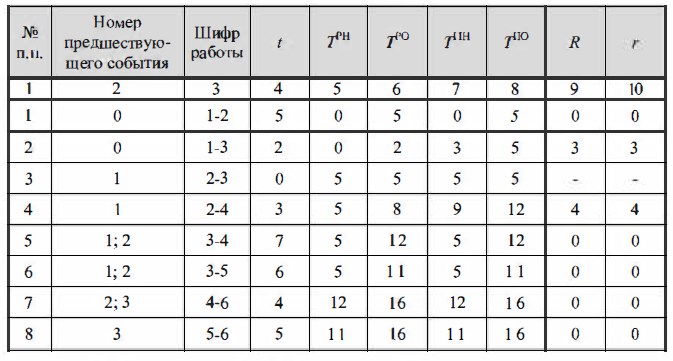
При расчете сетевых графиков табличным методом заполняют следующую таблицу (табл. 18.1).
Расчет сетевого графика
В графу 3 заносят шифр (код) каждой работы, запись ведут последовательно, начиная с первого события. Когда из события выходят несколько работ, запись ведут в порядке возрастания номеров их конечных событий. После этой процедуры в графу 2 записывают номера событий, предшествующих каждой работе.
Следующей заполняют графу 4. Против каждой работы, записанной в графе 3 из сетевого графика, проставляют её продолжительность t.
Максимальное раннее окончание последней работы равно величине критического пути.
Дальше заполняют графы 7 и 8. Позднее начало ТПН и окончание ТПО записываем в таблицу 18.1, начиная с конца графы.
Критический путь, а следовательно, и позднее окончание завершающей работы, равен 16 дням. Вносим эту цифру в строку 8 графы 8. Позднее начало работы равно разности его позднего окончания и продолжительности.
Общий резерв R (графа 9) определяют как разность между числами в графах 8 и 6 или 7 и 5.
Частный резерв r (графа 10) подсчитывают как разность между ранним началом последующей работы и ранним началом данной. При заполнении данной графы необходимо учитывать следующее, если в конечное событие данной работы входит только одна стрелка, то частный резерв ее равен нулю. Для работ, не лежащих на критическом пути, но входящих в события, лежащие на нем, общие и частные резервы численно равны. Частные и общие резервы работ, лежащих на критическом пути, равны нулю.
Правильность расчета сетевого графика подтверждают проверкой:
— ранние параметры никогда не превосходят по численному значению поздние параметры;
— критический путь должен представлять собой непрерывную последовательность работ от исходного события до завершающего;
— величина частного резерва времени работы не должна превосходить величину общего резерва времени;
— позднее начало одной из исходных работ обязательно должно быть нулевым.
Расчет сетевых графиков методом потенциалов
Потенциалом i-го события (ТjП ) называют величину наиболее продолжительного пути от данного события до завершающего:
Потенциал события (рис. 18.14) показывает, сколько дней осталось от данного события до завершения всех работ планируемой программы. Потенциал определяют последовательно, начиная от завершающего события сети.
В качестве примера рассмотрим тот же график, размещенный на рис. 18.13. Расчет (рис. 18.15) начинают с завершающего события 6, потенциал которого равен О. В верхний сектор ставим прочерк, в правый записываем О и переходим к последующему событию.
Рис. 18.14 Запись в секторах при расчете методом потенциалов
Рис. 18.15. Пример расчета методом потенциалов
( номера событий соответствуют рис. 18.1 З)
+ 3 = 7; выбирают наибольшее значение 11. Аналогичным образом рассчитывают остальные события. Потенциал исходного события составляет 16 дней, т.е. равен величине критического пути.
Зная потенциал события, позднее окончание работ можно определить по формуле
Поскольку ранние начала работ записаны в левых секторах, а на графике показаны продолжительности работ, по уже приведенным формулам частного и общего резерва времени можно определить их значение.
Изменения, возникающие в ходе выполнения работ, не влияют на потенциалы последующих событий; поэтому оперативный пересчет графика занимает мало времени. В этом заключается главное преимущество расчета методом потенциалов.
При этом методе каждое событие (рис. 18.16) графиком делится на 4 сектора, в которых указываются необходимые расчетные данные.
Рис. 18.16 Условные обозначения при четырехсекторном методе расчета
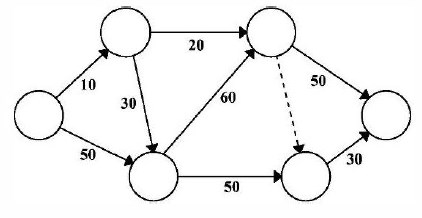
Исходным графиком для расчета четырехсекторным методом служит график, приведенный на рис. 18.17.
Рис. 18.17 Исходный график для расчета четырехсекторным методом
Вначале от исходного события до завершающего определяют все ранние начала работ.
Для завершающего события графика значения в левом и правом секторах равны, поскольку максимальное из ранних окончаний завершающей работы равно позднему окончанию этой работы.
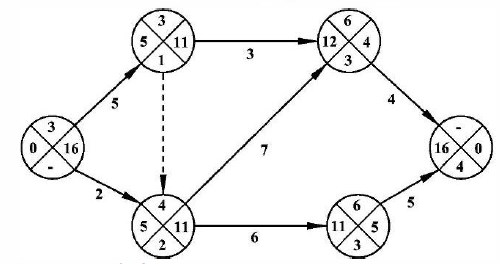
Затем рассчитывают поздние окончания работ от завершающего к начальному событию. Рассчитанный график будет иметь вид показанный на рис. 18.18.
Дополнительным требованием к критическим работам является требование по соблюдению условия
20-12 = 8; 25-5 = 20; 25-11 = 12; следовательно, работы нижнего пути- некритические.
Рис. 18.18 График, рассчитанный четырехсекторным методом
Резервы времени работ графика можно отметить на самом графике в виде Rr, а рассчитать их следует по формулам:
Четырехсекторный способ расчета сетевых графиков позволяет быстрее осуществить расчет и определить продолжительность критического пути (иногда требуется прикидочный расчет), но при повторном расчете требуется перебирать данные на графике. Этого не требуется при табличном способе, где пересчитывается сама таблица. Кроме того, в таблице наглядно прослеживаются все без исключения параметры сетевого графика (включая резервы времени).
Построение сетевых графиков «вершины-работы»
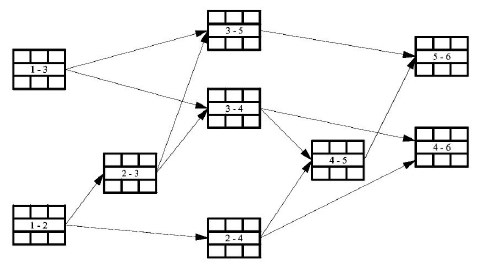
В последнее время построение сетевых графиков всё чаще выполняют по принципу «вершины-работы», а не по принципу «вершины-события», как это было в предыдущих примерах (рис.18.19).
Раннее начало последующей работы равно раннему окончанию предыдущей работы. Если работе непосредственно предшествует несколько работ, то ее раннее начало будет равно максимальному значению из ранних окончаний предшествующих работ.
Рис. 18.19 График типа «вершины-работы»
Рис. 18.20 Изображение работы в сетевом графике «вершины-работы»
Раннее окончание завершающей работы определяет продолжительность критического пути.
Расчет поздних сроков ведут в обратном порядке, от завершающей работы до исходной. Позднее окончание завершающей работы равно ее раннему окончанию, т.е. продолжительности критического пути.
Позднее начало определяют как разность позднего окончания и продолжительности работы.
Полный ( общий) резерв времени, равный разности поздних и ранних сроков, заносят в числитель середины нижней части.
Частный резерв времени, равный разности между минимальным ранним началом последующих работ и ранним окончанием данной работы, записывают в знаменатель середины нижней части.
Частный резерв всегда меньше полного резерва работы или равен ему. Последовательность работ с нулевыми резервами времени является критическим путем сетевого графика.
Построение сетевого графика: пример. Модель производственного процесса
Планирование работы всегда начинается с определения количества задач, ответственных за их исполнение лиц и времени, необходимого для полного завершения. При управлении проектами такие схемы просто необходимы. Во-первых, для того чтобы понимать, какое общее время будет затрачено, во-вторых, чтобы знать, как планировать ресурсы. Именно этим занимаются проектные менеджеры, они в первую очередь осуществляют построение сетевого графика. Пример возможной ситуации рассмотрим далее.
Исходные данные
Руководство рекламного агентства приняло решение о выходе в свет нового рекламного продукта для своих клиентов. Перед сотрудниками фирмы были поставлены такие задачи: рассмотреть идеи рекламных брошюр, привести аргументы в пользу того или иного варианта, создать макет, подготовить проект договора для клиентов и послать всю информацию руководству на рассмотрение. Для информирования клиентов необходимо провести рассылку, расклеить плакаты и обзвонить все фирмы, имеющиеся в базе данных.
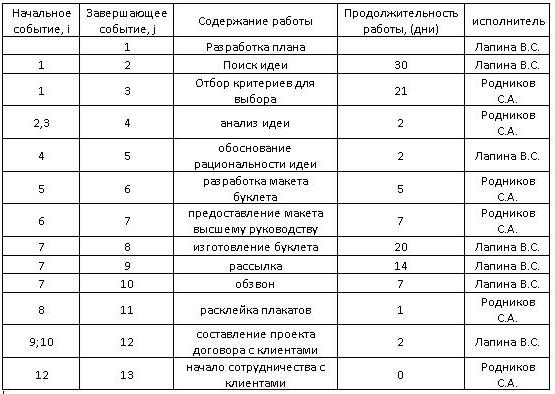
Кроме этого, главный руководитель составил детальный план всех необходимых действий, назначил ответственных сотрудников и определил время.
Начнем построение сетевого графика. Пример имеет данные, представленные на следующем рисунке:
Построение матрицы
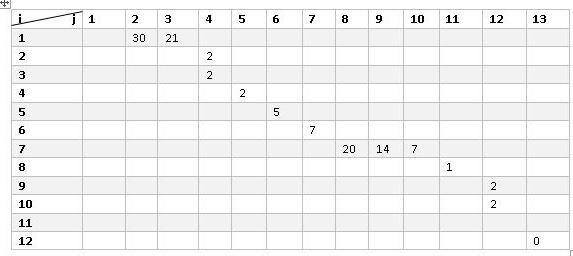
Перед тем как сформировать сетевой график, необходимо создать матрицу. Построение графиков начинается с этого этапа. Представим себе систему координат, в которой вертикальные значения соответствуют i (начальное событие), а горизонтальные строки – j (завершающее событие).
Начинаем заполнять матрицу, ориентируясь на данные рисунка 1. Первая работа не имеет времени, поэтому ею можно пренебречь. Рассмотрим детальнее вторую.
Начальное событие стартует с цифры 1 и заканчивается на втором событии. Продолжительность действия равняется 30 дням. Это число заносим в ячейку на пересечении 1 строки и 2 столбца. Аналогичным способом отображаем все данные, что представлено на рисунке ниже.
Основные элементы, используемые для сетевого графика
Построение графиков начинается с обозначения теоретических основ. Рассмотрим основные элементы, требующиеся для составления модели:
Работа может выполниться в трех состояниях:
— Действующая – это обыкновенное действие, на совершение которого требуются затраты времени и ресурсов.
— Ожидание – процесс, во время которого ничего не происходит, но он требует затрат времени для перехода от одного события к другому.
Основные принципы построения
Правила построения сетевых графиков заключаются в следующем:
Построение сетевого графика. Пример
Вернемся к исходному примеру и попробуем начертить сетевой график, используя все данные, указанные ранее.
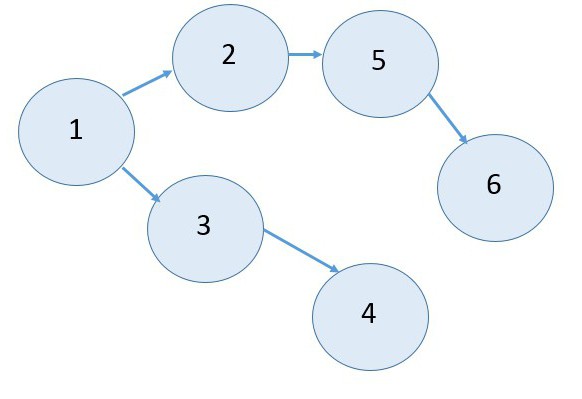
Начинаем с первого события. Из него выходят два – второе и третье, которые соединяются в четвертом. Далее все идет последовательно до седьмого события. Из него выходят три работы: восьмая, девятая и десятая. Постараемся все отобразить:
Критические значения
Это еще не все построение сетевого графика. Пример продолжается. Далее нужно рассчитать критические моменты.
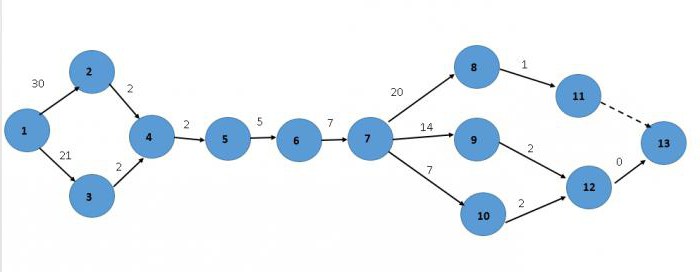
Критический путь – это наибольшее время, затраченное на выполнение задания. Для того чтобы его рассчитать, нужно сложить все наибольшие значения последовательных действий. В нашем случае это работы 1-2, 2-4, 4-5, 5-6, 6-7, 7-8, 8-11. Суммируем:
30+2+2+5+7+20+1 = 67 дней
Таким образом, критический путь равен 67 дням.
Если такое время на проект не устраивает руководство, его нужно оптимизировать согласно требованиям.
Автоматизация процесса
На сегодняшний день мало кто из проектных менеджеров вручную рисует схемы. Программа для построения сетевых графиков – это простой и удобный способ быстро рассчитать затраты времени, определить порядок работ и назначить исполнителей.
Кратко рассмотрим самые распространенные программы: