- Зачем нужны производные? Простое объяснение на примерах.
- Пример №1
- Пример №2
- Пример №3
- Применение производной. Построение графиков с применением производных
- Применение производной к исследованию функции
- Область определения и нули функции
- Возрастание и убывание
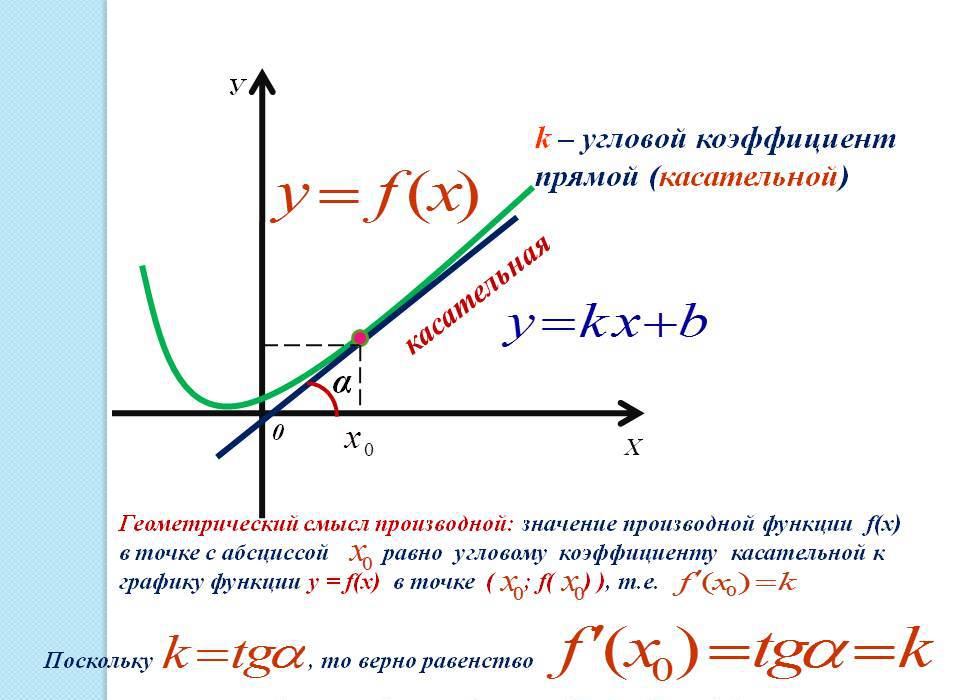
- Касательная и угловой коэффициент
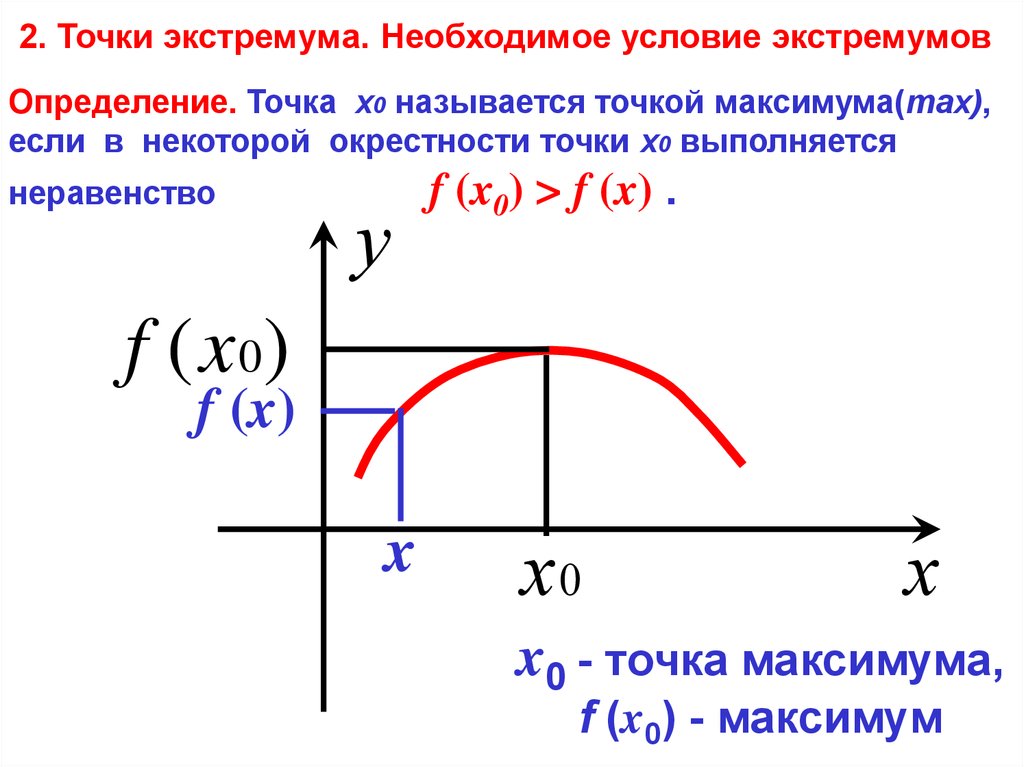
- Точки экстремума
- Выпуклости и вогнутости
- Частные производные
- Производная в физике
- Производная в химии и биологии
- Производная в географии и экономике
- Заключение
- «ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ»
Зачем нужны производные? Простое объяснение на примерах.
Здравствуй, дорогой читатель.
Не забудь про лайк, если было интересно!
Да, большинству из нас производные вообще не нужны, но это не значит, что у них нет применения. Наоборот. Производные всюду вокруг нас!
И чтобы показать, что на самом деле производной пользуются в очень многих областях науки, рассмотрим несколько очень простых примеров.
Пример №1
Допустим, решили Вы заняться спортом и отжимаетесь каждый день. Составили табличку и записываете туда свои результаты. В конце недели решили проанализировать, как росли результаты и составили график.
Другими словами, скорость роста нашей функции равна нулю.
На следующей неделе Вы собрались с духом и результаты пошли в гору.
Ну теперь явно видно, что наши результаты росли по 5 отжиманий в день, а значит, скорость роста функции, или производная равна 5.
И очень часто бывает так, что нужно найти какое-то максимальное или минимальное значение функции, здесь нам и помогает производная. Достаточно всего лишь найти корни, приравняв её к нулю.
Пример №2
Допустим, у нас в распоряжении 26 секций забора и нужно расположить эти секции таким образом, чтобы получить прямоугольник наибольшей площади.
Можно конечно пуститься во все тяжкие и начать перебирать, но можно и доказать, что на алгебре мы не зря штаны протирали 🙂
Далее, находим площадь фигуры, благо это не сложно.
Мы на полпути к успеху. Теперь, берем производную по площади и приравниваем её к нулю.
Получается, что наибольшую площадь будет иметь квадрат со стороной 6,5.
Трудно оценить, насколько эта задача «жизненная», но как по мне, ярко иллюстрирует, что знание даже базовых понятий о производной может сильно упростить жизнь.
В комментариях обязательно кто-нибудь напишет, что сторону квадрата достаточно было найти делением периметра на четыре. Но я-то здесь говорю о производной.
Ну и последняя задачка.
Пример №3
Завод по производству резиновых изделий выпускает какое-то количество средств контрацепции в неделю, и известно, что полученная прибыль в итоге выражается формулой:
Вопрос: какое максимальное количество продукции нужно производить в неделю, чтобы получить максимальную прибыль?
И снова обращаемся к производной.
Напишите в комментариях, пригодилось ли Вам в жизни знание производных?
Понять что такое производная мне помог канал на ютьюб «QWERTY».
Применение производной. Построение графиков с применением производных
Математика берет свои истоки со времен Античности. Благодаря ней архитектура, строительство и военное дело дали новый виток развития, достижения, которые были получены с помощью математики, привели к движению прогресса. И по сей день математика остается главной наукой, которая встречается во всех остальных отраслях.
Применение производной к исследованию функции
Область определения и нули функции
Нули функции находятся простым способом: функцию f(x) следует приравнивнять к нулю и решить полученное уравнение относительно одной переменной x. Полученные корни уравнения являются нулями функции, то есть в этих x функция равна 0.
Возрастание и убывание
Касательная и угловой коэффициент
Геометрический смысл производной: производная функции f(x) равняется угловому коэффициенту образованной касательной к графику этой функции в данной точке x. Угловой коэффициент, в свою очередь, равняется тангенсу угла наклона касательной к оси ОХ (абсцисс) в положительном направлении. Это следствие является основополагающим к применению производной к графику функции.
Точки экстремума
Применение производной к исследованию включает в себя нахождение точек максимума и минимума.
Для того чтобы найти и определить точки минимума и максимума, необходимо:
Чтобы найти экстремумы функции:
Выпуклости и вогнутости
Определить выпуклость и вогнутость можно, прибегая к применению производной для построения графиков:
Точка, которая разделяет выпуклость и вогнутость, называется точкой перегиба функции.
Чтобы найти точки перегиба:
Частные производные
Производная в физике
С помощью применения производной находятся такие величины:
Производная в химии и биологии
Производная в географии и экономике
Производная позволяет географам решать такие задачи, как нахождение численности населения, вычислять значения в сейсмографии, рассчитать радиоактивность ядерно-геофизических показателей, вычислить интерполяцию.
В экономике важную часть расчетов занимает дифференциальное исчисление и вычисление производной. В первую очередь это позволяет определить пределы необходимых экономических величин. Например, наибольшую и наименьшую производительность труда, издержки, прибыль. В основном эти величины рассчитываются по графикам функций, где находят экстремумы, определяют монотонность функции на нужном участке.
Заключение
«ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ»
Глава I. Применение производной в практической деятельности……………………….….3
ГЛАВА II. ПРОИЗВОДНАЯ В ЭКОНОМИЧЕСКИХ ЗАДАЧАХ……………………………..………………7
§1. Понятие производственной функции…………………………………………….7
§4. Постановка и решение основной задачи……………………………….………11
ГЛАВА III. ПРИМЕНЕНИЯ ПРОИЗВОДНОЙ В ДОКАЗАТЕЛЬСТВЕ НЕРАВЕНСТ………….……..…..14
§1. Несколько простых примеров……………………………………………….…..14
§2. От числовых неравенств – к функциональным…………………………..…….15
§3. Неравенства с несколькими переменными………………………………..……15
§4. Доказательство неравенств Гюйгенса……………………………. ……..…….17
Введение
В процессе изучения производной в школьном курсе математики рассматриваются некоторые её приложения в физике, а также ряд текстовых задач на нахождение наибольшего или наименьшего значений. Однако сфера производной применения этим не ограничивается. Например, существует масса реальных экономических задач, для решения которых необходимо использовать методы дифференциального исчисления.
Метод нахождения экстремальных значений функции имеет важнейшее, ключевое значение для решения большого класса задач из разных разделов курса физики, математики, экономики и других наук. Специфика этих задач включает получение на основе некоторых физических и математических закономерностей функциональной зависимости и нахождение экстремального значения. В наше время, в связи с научно-техническим прогрессом, в частности с быстрой эволюцией вычислительных систем, дифференциальное исчисление становится все более актуальным в решении как простых, так и сверхсложных задач.
Цель: исследовать применение производной в различных областях науки и техники.
Задачи: 1)рассмотреть применение производной в практической деятельности;2) подбор физических и экономических задачи на экстремум; 3) показать применение производной к выяснению истинности неравенств.
Методы исследования: анализ и решение, сравнение результатов с реальной действительностью.
Каждый человек время от времени оказывается в ситуации, когда надо отыскать наилучший способ решения какой-либо задачи, и математика становится средством решения проблем организации производства, поисков оптимальных решений. Важным условием повышения эффективности производства и улучшения качества продукции является широкое внедрение математических методов в технику. Среди задач математики большую роль отводят задачам на экстремумы, т.е. задачам на отыскание наибольшего и наименьшего значения, наилучшего, наиболее выгодного, наиболее экономного. С такими задачами приходиться иметь дело представителям самых разных специальностей: инженеры-технологи стараются так организовать производство, чтобы получилось как можно больше продукции, конструкторы хотят так спланировать прибор на космическом корабле, чтобы масса прибора была наименьшей, экономисты стараются спланировать прикрепление заводов к источникам сырья так, чтобы транспортные расходы оказывались минимальными.
ГЛАВА I. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ В ПРАКТИЧЕСКОЙ ДЕЯТЕЛЬНОСТИ
§1. Геодезия
В «Геометрии 6-9» указан способ определения высоты предмета с помощью угломерных инструментов. При типографических съемках местности аналогичный приём используется для определения превышения одной точки земной поверхности над другой. Этот способ дает хороший результат, если рассматриваемые точки находятся на незначительном расстоянии. В противном случае начинает сказываться кривизна Земли и возникает существенная погрешность.
§2. Транспорт
В практике проектирования сети автомобильных дорог часто возникает необходимость устройства узла разветвления. Местоположение узла и взаимное расположение проходящих через него дорог определяется комплексом экономических и географических условий, но первый, предварительный этап решение этой задачи учитывает лишь затраты рабочего времени на перевозки, причём в качестве вспомогательной решается вначале следующая задача.
§3. Мелиорация
Площадь поперечного сечения канала называют его живым сечением, а длину границы такого сечения называют смоченным периметром канала. С помощью теоретических расчетов и эксперимента установлено, что из всех каналов с заданным живым сечением наибольшей пропускной способностью и одновременно наименьшей фильтрацией отличаются каналы с наименьшим смоченным периметром. Про такие каналы говорят, что они имеют гидравлически наивыгоднейший профиль.
В мелиоративной практике часто сооружаются каналы или лотки с поперечным сечением в форме прямоугольника, треугольника, трапеции и сегмента круга. Поэтому представляет интерес расчет гидравлически наивыгоднейшого профиля для каналов такой формы.
Итак, проверяемое утверждение справедливо.
§2. От числовых неравенств – к функциональным
Иногда требуется решить задачу, которая связана с числовыми неравенствами и в условии которой о дифференцируемых функциях нет речи; и тем не менее в подобной ситуации нередко оказывается выгодным перейти к подобранной «функциональной» задаче, которая решается с помощью производной и из ее решения уже следует решение исходной задачи.
Решение. Все эти задачи сводятся к такой вспомогательной функциональной задаче.
§3. Неравенства с несколькими переменными
Пример 7. Проверить, справедливо ли при любых положительных a, b, c неравенство (3).
Для выяснения истинности неравенства иногда удобно воспользоваться следующим утверждением, которое непосредственно вытекает из теоремы 1:
§4. Доказательство неравенств Гюйгенса
Заключение
Математика служит основой естественных и технических наук, без нее ныне не мыслима ни одна современная технология. Кроме того, математика активно внедряется в экономику. Приступая к данному исследованию, мы ставили перед собой задачу: применение производной на нахождение экстремальных значений функции в различных областях практической деятельности. Для этого:
были выбраны задачи из сборников задач по физике и подготовке к единому государственному экзамену, в которых требовалось найти наименьшее или наибольшее значение;
выполнено решение подобранных задач;
выполнена классификация задач по разделам физики, математики и экономики.
Применение производной довольно широко и его сложно полностью охватить в работе такого типа, однако, мы попытались раскрыть основные, базовые моменты. В наше время, в связи с научно-техническим прогрессом, в частности с быстрой эволюцией вычислительных систем, дифференциальное исчисление становится все более актуальным в решении как простых, так и сверхсложных задач. Можно сказать, что задачи на отыскание наименьшего и наибольшего значения, имеют большое практическое применение. В данной работе показано решение таких задач.
Литература
Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В., Федорова Н.Е., Шабунин М.И. Алгебра и начала анализа 10-11 классы, М., Просвещение, 2003.
Балк М.Б. Применение производной к выяснению истинности неравенств. – Журнал «Математика в школе», №6, 1975, с. 47-53.
Беденко Н.К., Вольдман М.С. Некоторые задачи с техническим содержанием по теме «Производная и ее применениеехническим содержанием поноических задач ости000000000000000000000000000000000000000000000000000000000000000». – Журнал «Математика в школе», №5, 1975, с. 49-52.
Бодрякова Н.О., Рыб К.А. Физические задачи на экстремум функции. – Журнал «Математика в школе», №3, 1993, с. 15-20.
Игнатьева Н.П., Симонов А.С.. Об одном приложении производной к решению экономических задач. – Журнал «Математика в школе», №9, 2001, с. 42-48.
Москалев А.Н., Никулова Г.А. Готовимся к единому государственному экзамену. Физика. М., Дрофа, 2007.
Петров В.А, Чертков В.С. Применение производной в практической деятельности. – Журнал «Математика в школе», №6, 1980, с. 30-32.
Рымкевич А.П. Физика. Задачник 10-11 классы. М., Дрофа, 2007.