Применение теории матриц в строительных расчетах
Конечные элементы, из которых собирается расчетная схема любой конструкции, имеют общие характеристики. Так, для любого конечного элемента определяющим является число его степеней свободы, то есть общее число всех возможных перемещений во всех узлах конечного элемента. При этом для элемента одного типа можно учитывать как все, так и лишь некоторые из возможных перемещений в узле. Количество учитываемых узловых перемещений определяется контекстом решаемой задачи.
Выбор типов конечных элементов для моделирования конструкции определяется в первую очередь особенностями исходной системы. В каждом конкретном случае для моделирования системы выбираются соответствующие конечные элементы с числом и характером степеней свободы (узловых перемещений), определяющих основные особенности работы системы.
В зависимости от числа учитываемых в расчете степеней свободы в узле конечного элемента формируется матрица жесткости конечного элемента.
Матрица жесткости представляет собой универсальный математический объект, используемый в методе конечных элементов для описания упругих свойств как отдельных элементов, так и более крупных частей рассматриваемой системы, а также всей системы целиком. Матрица жесткости может быть составлена и для бесконечно малого элемента.
По определению матрица жесткости представляет собой таблицу значений реакций в связях узлов конечного элемента от единичных перемещений, последовательно задаваемых по направлению этих связей.
Фактически матрица коэффициентов при неизвестных канонических уравнений метода перемещений представляет собой матрицу жесткости конструкции.
Если обратиться к таблицам традиционного метода перемещений, легко заметить, что в них содержатся элементы матрицы жесткости стержневого конечного элемента b.
Порядок матрицы жесткости определяется числом учитываемых степеней свободы конечного элемента. Для конечного элемента a с двумя степенями свободы в каждом узле (это линейные перемещения по направлению каждой из осей системы координат) порядок матрицы жесткости (4×4).
Для конечного элемента b, также имеющего две степени свободы в узле (линейное вертикальное перемещение и угол поворота),
порядок матрицы, как и в предыдущем случае, (4 × 4).
Для конечного элемента c с тремя степенями свободы в узле (двумя линейными перемещениями по направлению осей координат и углом поворота) порядок матрицы жесткости (6 × 6). Заметим, что элемент c объединяет элементы a и b. Тем не менее все рассматриваемые конечные элементы имеют право на самостоятельное существование.
Конечный элемент d используется для расчета тонких плит. В каждом узле такого конечного элемента учитываются три степени свободы. Порядок матрицы жесткости элемента (12 × 2).
Последний конечный элемент e может быть использован для расчета массивных конструкций. В каждом узле такого элемента учитывается шесть степеней свободы.
Введение. Матрицы в строительной механике
Ю.Г.Плотников
Матрицы в строительной механике
Кафедра «Механика деформируемого твердого тела»
Тихоокеанского государственного университета
(заведующий кафедрой, кандидат технических наук,
Доктор технических наук, профессор, заведующий кафедрой
«Механика деформируемого твердого тела»
Дальневосточного государственного технического университета
Плотников Ю.Г.
Матрицы в строительной механике: учеб. пособие. – Хабаровск: Изд-во ДВГУПС, 2008. – 111 с: ил.
Учебное пособие соответствует ГОС ВПО направлений подготовки дипломированных специалистов: 270100 «Строительство», 270200 «Транспортное строительство» специальностей: 270102 «Промышленное и гражданское строительство»; 270201 «Мосты и транспортные тоннели» по дисциплине «Строительная механика».
Учебное пособие содержит изложение материала о применении теории матриц в расчетах строительных конструкций. Приведены матричные методы определения перемещений, матричная форма метода сил и метода перемещений, матричный метод проф. А.Ф.Смирнова для определения критической нагрузки в теории устойчивости сооружений, матричные методы решения задач динамики сооружений. Завершает изложение применение теории матриц в методе конечных элементов. Теоретический материал сопровождается решением примеров.
Предназначено для студентов всех форм обучения.
Z ГОУ ВПО «Дальневосточный государственный
Университет путей сообщения» (ДВГУПС), 2008
Введение
Настоящее пособие включает разделы строительной механики, в которых излагаются методы статического и динамического расчета сооружений использующие матричные методы. Представленный материал соответствует действующим в настоящее время учебным программам для строительных и транспортных специальностей.
Развитие строительной механики в настоящее время связано с применением в расчетах строительных конструкций мощных персональных компьютеров (ПК). В связи с этим в теорию расчетов все шире внедряются, использующие удобные для реализации на ПК матричные методы. В настоящее время каждый инженер-расчетчик имеет в своем распоряжении мощный персональный компьютер, который может выполнить любой расчет по программам, написанным на основе методов строительной механики. В свою очередь методы строительной механики требуют перед программированием описания задачи в матричной форме, поскольку язык матричной алгебры оказался наиболее удобным для общения человека с электронно-вычислительной машиной.
Студенты, обучающиеся на инженерно-строительных специальностях, по мере изучения различных дисциплин впервые встречаются с теорией матриц в курсе высшей математики, где им даются основные понятия матричной алгебры. Там же показано применение теории матриц к решению систем линейных алгебраических уравнений. Это все, что дает курс высшей математики будущему инженеру строителю. Для изучения строительной механики этих сведений, полученных на первом курсе обучения явно недостаточно. Поэтому в данном пособии в начале кратко изложен материал матричной алгебры, известный из курса высшей математики, а именно сложение, умножение и обращение матриц. Далее излагаются понятия собственных чисел и собственных векторов матриц. Формулируется полная проблема собственных значений матриц. Дается один из методов решения этой проблемы – метод итераций.
В пособии изложены следующие матричные методы: теория перемещений, методы статического расчета: методы сил и перемещений, определение критической нагрузки при расчете на устойчивость, методы динамического расчета конструкций при действии гармонической и произвольной нагрузки.
Последний раздел посвящен использованию теории матриц в методе конечных элементов. Здесь также рассмотрено решение статических задач, задач устойчивости и динамики стержневых систем.
Организация, управление и планирование в строительстве
Расчет разноритмичного потока с использованием матрицы
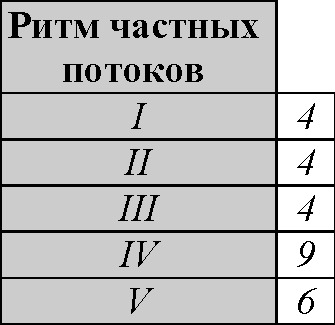
В исходных данных к заданию указаны ритмы частных потоков. Ритм частных потоков – это ритм работы бригады – продолжительность работы на одной захватке.
Исходные данные к расчету разноритмичного потока
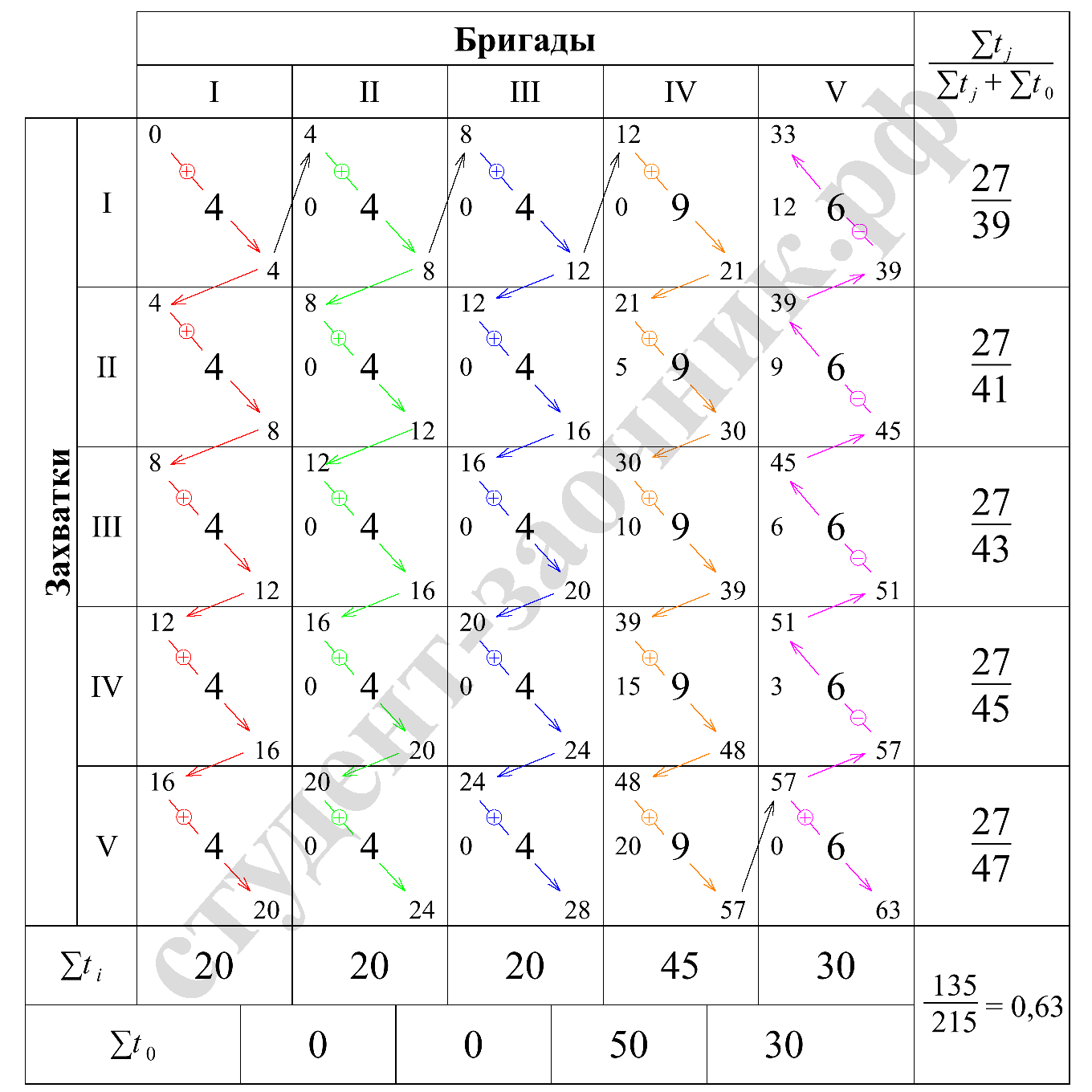
Заполняем клетки матрицы продолжительностями работ учитывая, что у каждой бригады на всех захватках ритм работы одинаков.
Рис. 1 Расчет параметров разноритмичного потока с помощью матрицы
Определяем ∑ti суммируя продолжительность работ бригады на каждой захватке.
Продолжительность работ на всех захватках:
I бригады ∑ti = 4 + 4 + 4 + 4 + 4 = 20 дней;
II бригады ∑ti = 4 + 4 + 4 + 4 + 4 = 20 дней;
III бригады ∑ti = 4 + 4 + 4 + 4 + 4 = 20 дней;
IV бригады ∑ti = 9 + 9 + 9 + 9 + 9 = 45 дней;
V бригады ∑ti = 6 + 6 + 6 + 6 + 6 = 30 дней.
Полученные значения ∑ti записываем в предпоследнюю строку матрицы.
Определяем ∑tj суммируя продолжительность работ всех бригад на отдельной захватке. Для разноритмичного потока ∑tj на каждой захватке будет одинаковой. В нашем примере ∑tj = 4 + 4 + 4 + 9 + 6 = 27 дней. Полученные значения ∑tj записываем в соответствующую строку правого столбца матрицы над чертой.
Заполняем время начала и окончания работ на захватке. Заполнение начинаем с первой клетки (пересечение первой строки и первого столбца) матрицы. Для этого в левый верхний угол первой клетки матрицы заносим время начала работ, для I бригады на I захватке – это 0. В правый нижний угол первой клетки матрицы заносим время окончания работ бригады на захватке суммируя время начала работ на захватке и продолжительность работ, для I бригады на I захватке – это 0 + 4 = 4 дня.
Переходим к второй клетке (пересечение второй строки и первого столбца) матрицы заполняя ее левый верхний угол. Временем началом работы на II захватке считается время окончания работ на I захватке, следовательно, значение из правого нижнего угла первой клетки матрицы переносится в левый верхний угол второй клетки матрицы. Заполняем правый нижний угол второй клетки матрицы суммируя время начала работы и продолжительность работ, для I бригады на II захватке – это 4 + 4 = 8 дней. Аналогичным образом поступаем для всех остальных захваток I бригады.
Расчет времени начала и окончания работ на захватках для других бригад ведут в зависимости от продолжительности работ. Если продолжительность работы последующей бригады больше или равна предыдущей, то заполнение столбца матрицы проводят сверху вниз, если меньше, то снизу верх. В нашем примере продолжительность работ I и II бригады равны (20 = 20), следовательно, временем начала работы II бригады на I захватке, будет время окончания работ I бригады на I захватке, значение из правого нижнего угла первой клетки матрицы переносим в левый верхний угол клетки находящейся на пересечении первой строки и второго столбца матрицы. Дальнейшее заполнение значений до четвертого столбца включительно подобно первому столбцу матрицы. Продолжительность работ IV бригады больше продолжительности работ V бригады (45 > 30), следовательно, заполнение пятого столбца матрицы проводим снизу вверх. Время начала работ V бригады на V захватке будет время окончания работ IV бригады на V захватке, записываем это значение в левый верхний угол клетки находящейся на пересечении пятой строки и пятого столбца матрицы. Это значение также является временем окончания работ V бригады на IV захватке, поэтому переносим его в правый нижний угол вышележащей клетки матрицы. Расчет времени начала и окончания работ проводим в обратном порядке вычитая из времени окончания работ продолжительность работ (направление заполнения значений указанно на рис. 1 фиолетовыми стрелками).
После заполнения всех значений времени начала и окончания работ на каждой захватке приступаем к определению значений t0 – продолжительности перерывов в работе смежных бригад на захватках. Величина простоя определяется, как разность времени начала работ последующей бригады и временем окончания работ предыдущей бригады на данной захватке. В нашем примере продолжительность перерывов в работе смежных бригад составляет:
На I захватке для IV и V бригады t0 = 33 – 21 = 12 дней;
На III захватке для III и IV бригады t0 = 30 – 20 = 10 дней;
На IV захватке для IV и V бригады t0 = 51 – 48 = 3 дня.
Далее суммируем продолжительности перерывов в работе у смежных бригад:
— по строкам матрицы определяя общую продолжительность простоя фронта работ на всех захватках. В нашем примере общая продолжительность перерывов между окончанием работ на захватках III бригады и налом работ на захватках IV бригады составляет ∑t0 = 0 + 5 + 10 + 15 + 20 = 50 дней. Полученные значения ∑t0 записываем в нижнюю строку матрицы;
— по столбцам матрицы определяя общую продолжительность простоя фронта работ на отдельной захватке. В нашем примере общая продолжительность перерывов в работе на III захватке составляет ∑t0 = 0 + 0 + 10 + 6 = 16 дней.
Суммируем полученные ранее значения ∑tj и ∑t0 записываем в соответствующую строку правого столбца матрицы под чертой. Определяем С – степень эффективности запроектированных потоков по формуле C = ∑∑tj/(∑∑tj+∑∑t0). В нашем примере С = (27 + 27 + 27 + 27 +27)/(39 + 41 + 43 + 45 + 47) = 135/215 = 0,63
Расчет неритмичного потока с использованием матрицы
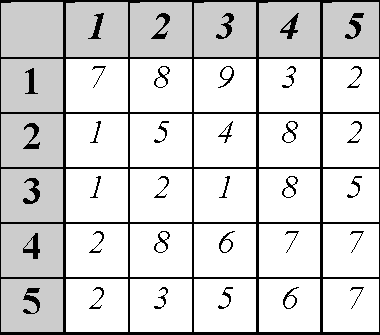
Исходные данные к расчету неритмичного потока
Расчет неритмичного потока начинаем с заполнения клеток матрицы продолжительностями работ согласно заданию.
Определяем ∑ti суммируя продолжительность работ бригады на каждой захватке.
Продолжительность работ на всех захватках:
I бригады ∑ti = 7 + 8 + 9 + 3 + 2 = 29 дней;
II бригады ∑ti = 1 + 5 + 4 + 8 + 2 = 20 дней;
III бригады ∑ti = 1 + 2 + 1 + 8 + 5 = 17 дней;
IV бригады ∑ti = 2 + 8 + 6 + 7 + 7 = 30 дней;
V бригады ∑ti = 2 + 3 + 5 + 6 + 7 = 23 дней.
Полученные значения ∑ti записываем в предпоследнюю строку матрицы.
Определяем ∑tj суммируя продолжительность работ всех бригад на отдельной захватке:
I захватка ∑tj = 7 + 1 + 1 + 2 + 2 = 13 дней;
II захватка ∑tj = 8 + 5 + 2 + 8 + 3 = 26 дней;
III захватка ∑tj = 9 + 4 + 1 + 6 + 5 = 25 дней;
IV захватка ∑tj = 3 + 8 + 8 + 7 + 6 = 32 дня;
V захватка ∑tj = 2 + 2 + 5 + 7 + 7 = 23 дня.
Полученные значения ∑tj записываем в соответствующую строку правого столбца матрицы над чертой.
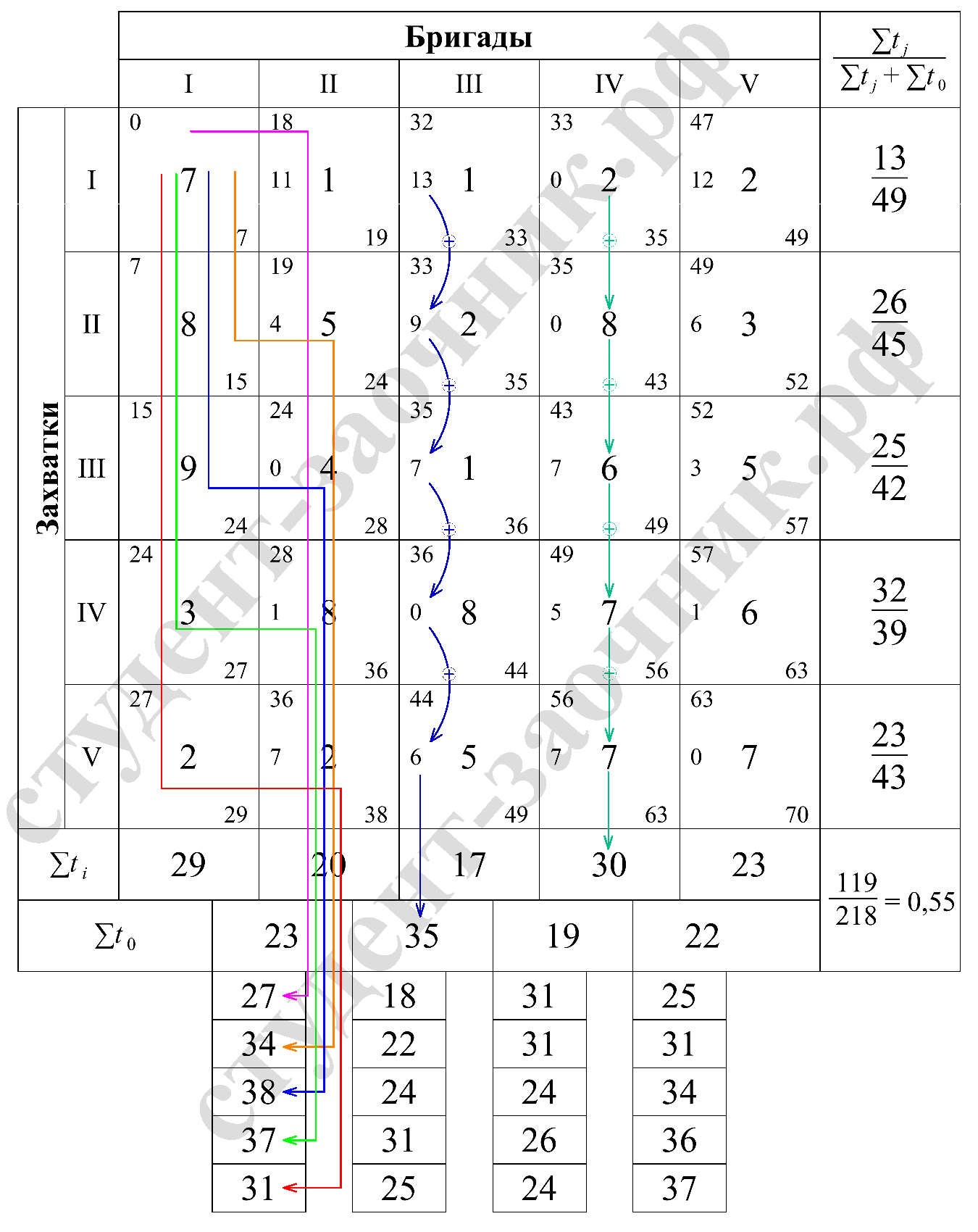
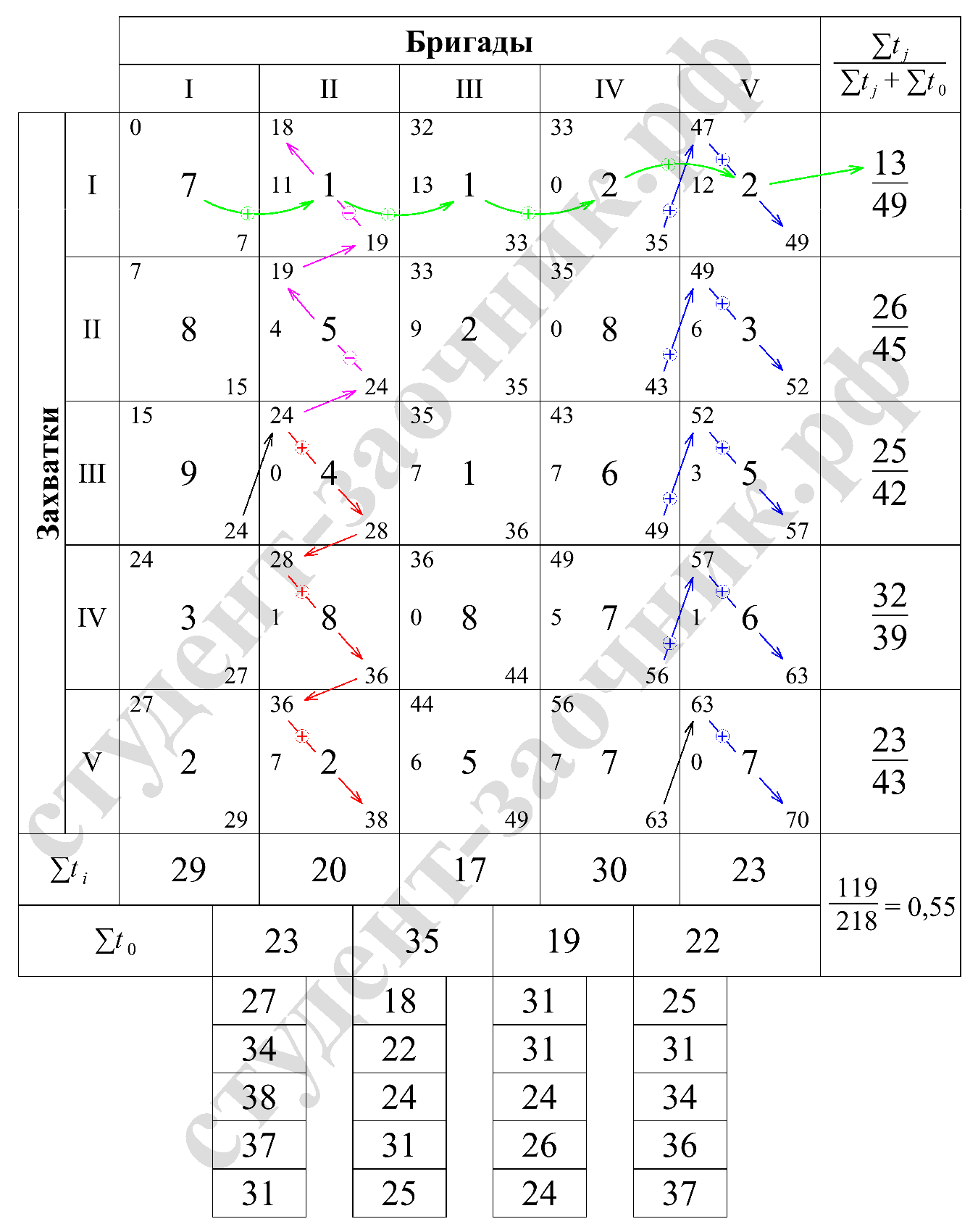
Рис. 2 Расчет параметров неритмичного потока с помощью матрицы
Определяем ∑ti суммируя продолжительность работ бригады на каждой захватке.
Заполняем время начала и окончания работ на захватке. Заполнение начинаем с первой клетки (пересечение первой строки и первого столбца) матрицы. Для этого в левый верхний угол первой клетки матрицы заносим время начала работ, для I бригады на I захватке – это 0. В правый нижний угол первой клетки матрицы заносим время окончания работ бригады на захватке суммируя время начала работ на захватке и продолжительность работ, для I бригады на I захватке – это 0 + 7 = 7 дней. Дальнейшее заполнение значений первого столбца матрицы ведем сверху вниз аналогично заполнению первого столбца матрицы для расчета разноритмичного потока.
Переходим к увязке I и II бригады. Определим места критических сближений для этого находим наибольшую продолжительность выполнения работ на захватках этими бригадами путем суммирования продолжительностей работ. Предположим, что критическое сближение находится на I захватке, тогда продолжительность выполнения работ TI = 7 + 1 + 5 + 4 + 8 + 2 = 27 дней. Аналогично выполняем те же самые операции, предполагая, что критическое сближение находится на II, III, IV, V захватке:
TII = 7 + 8 + 5 + 4 + 8 + 2 = 34 дня;
TIII = 7 + 8 + 9 + 4 + 8 + 2 = 38 дней;
TIV = 7 + 8 + 9 + 3 + 8 + 2 = 37 дней;
TV = 7 + 8 + 9 + 3 + 2 + 2 = 31 день.
Полученные значения записываем в столбец под последней строкой матрицы между столбцами I и II бригады.
Рис. 3 Расчет параметров неритмичного потока с помощью матрицы
Максимальная продолжительность показывает место критического сближения, в нашем примере это 38, следовательно, III захватка является критической. На этой захватке процесс начинается без задержки, поэтому время окончания выполнения работ I бригады III захватке является временем начала работ II бригады III захватке.
Далее заполнение столбца значениями времени начала и окончания работ на захватках возможно двумя способами:
1) Заполнение столбца матрицы начиная от значения времени начала работ II бригады III захватке проводят сверху вниз до значения окончания работ II бригады V захватке и снизу верх до значения начала работ II бригады I захватке. После этого вычисляются значения продолжительности перерывов в работе смежных бригад на захватках подобно рассмотренному выше расчету разноритмичного потока.
2) Первоначально вычисляются значения продолжительности перерывов в работе смежных бригад на захватках путем вычитания из максимального значения продолжительности выполнения работ значений указанных в столбце под последней строкой матрицы:
I захватка t0 = Tmax – TI = 38 – 27 = 11 дней;
II захватка t0 = Tmax – TII = 38 – 34 = 4 дня;
III захватка t0 = Tmax – TIII = 38 – 38 = 0;
IV захватка t0 = Tmax – TIV = 38 – 37 = 1 день;
V захватка t0 = Tmax – TV = 38 – 31 = 7 дней.
Полученные значения t0 записываем в матрицу, далее вычисляем значения времени начала работ на захватке путем сложения значений времени окончания работ предыдущей бригадой на данной захватке и продолжительностью перерыва. Значения времени окончания работ на захватке определяем аналогично первому столбцу матрицы.
Вычисление остальных параметров потока не отличается от разноритмичного потока, рассмотренного выше.