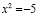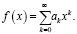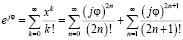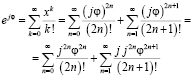Применение комплексных чисел в строительстве

В математике чрезвычайно обширно используется решение задач с помощью комплексных чисел. Однако, что такое комплексные числа и как они нашли себя в электротехнике [4]?

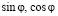
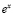
Для начала рассмотрим формулу Эйлера. Это серьёзная и важная формула, которая объединяет тригонометрические функции с экспонентой – с функцией, которая не входит в состав периодических функций, но очень часто используется в электротехнике [1].

Формула Эйлера считается базовой формулой при вычислении комплексных напряжений токов в электротехнике [2 ].

Известно, что свойства большинства математических функций выводят на множестве вещественных чисел, если они на этом множестве существуют. Но, например, уравнение

решения в области вещественных чисел не имеет.

Для того чтобы обеспечить решение таких уравнений, было введено понятие комплексного числа, включающего в себя не только вещественную, но и мнимую часть, которая содержит мнимую единицу, по определению равную

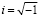
Если ввести допущение, что такое число существует, то всё равно очень много математических функций при невыполнении не выводят за множество комплексных чисел, а продолжают рассматривать на множестве вещественных чисел. При этом остаётся немало задач, особенно прикладного характера, решение которых нужно производить с помощью комплексных чисел [5, 6, 8].

Комплексным числом Z в общем случае считают сумму пары чисел – вещественного числа x и произведения yi, где i – есть мнимая часть:

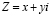
Преимуществом комплексных чисел является то, что, практически, все математические операции над комплексными числами не выходят за множество комплексных чисел, то есть результат действия над комплексными числами можно выразить в виде комплексного числа.

Этим активно пользуются при расчётах в электротехнике. В математике для символического изображения мнимой единицы используют обозначение i, но в электротехнике же так принято обозначать ток, поэтому это обозначение заменяют на j, физический смысл же от этого не меняется:

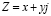
Вернёмся, применив эту формулу к тригонометрическим функциям, а именно к .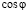

Учтём, что любая функция f(x) при определённых условиях представима в виде степенного ряда, то есть сводится к виду

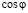
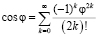
При разложении функции в ряд Маклорена получим:

Также распишем ряд Маклорена для функции :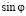

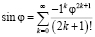
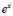
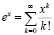
Точно так разложим на ряд Маклорена функцию и получим:

Предположим, что х принадлежит множеству комплексных чисел и 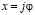. Для того, чтобы получить формулу Эйлера разобьём этот ряд на два ряда по чётным и нечётным степеням k:

далее в первом и втором слагаемом путём элементарных преобразований вынесем за скобку 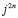и получим:

Учитывая то, что 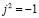, то получим следующее:

Собственно говоря, мы получили формулу Эйлера, устанавливающую зависимость между экспонентой и тригонометрическими функциями и имеющую вид:

Эта формула существенно помогает упростить математические выражения в комплексной области. Так при описании электромагнитных процессов в цепях переменного тока приходится вычислять много непростых интегралов, что приводит к громоздкому решению. Оказалось, что выполнение поставленных задач упрощается при введении комплексных чисел [3, 7].

Комплексные числа можно представлять в разных формах записи – алгебраической, тригонометрической или показательной – в зависимости от постановки задачи, исходных данных и требуемых результатов, но благодаря формуле Эйлера легко переходить от одной формы записи к другой. Например, переменный ток в цепи можно записать по-разному:

– алгебраическая форма;

= – тригонометрическая форма;

= – показательная форма.

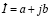
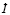
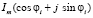
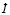
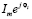
При сложении токов в цепях с начальной фазой, равной нулю, сложностей не возникает. Но при сложении токов с разными начальными фазами простая, на первый взгляд, задача приводит к громоздким тригонометрическим вычислениям. Тогда как, используя переход к комплексным числам, эта же задача решается в несколько строк [9, 10].

Если решать задачи электротехники с помощью векторов, то опять же удобно перейти к комплексной записи токов или напряжений и выполнять построения на комплексной плоскости, где горизонтальная ось – ось вещественной части комплексного числа, а вертикальная – ось мнимой части этого же числа.

Комплексные числа также применяются для описания гармонических колебаний в линейных электрических цепях, при этом переход от реальных гармонических токов и напряжений к комплексным амплитудам выражает суть метода комплексных амплитуд, который является моделью исследуемых процессов, где на первое место выдвигаются амплитуды, а время и частоты отодвигаются на задний план. Переход к комплексным значениям позволяет компактно описать один объект сразу двумя величинами.

По сути, переход от реальных гармонических колебаний к комплексным амплитудам есть построение модели с помощью комплексных чисел, которые в этой модели носят названия – комплексный ток, комплексное напряжение, комплексная ЭДС.

Применение комплексных чисел позволяет:

– использовать законы, формулы и методы расчётов, применяющиеся в цепях постоянного тока, для расчёта цепей переменного тока;

– упростить некоторые вычисления, заменив графическое решение с использованием векторов на алгебраическое решение;

– рассчитывать сложные цепи, не решающиеся другим путем;

– упростить расчеты цепей постоянного и переменного токов.

Источник

Где применяются комплексные числа?

В течение последних двухсот лет комплексные числа находят многочисленные, а иногда и совершенно неожиданные применения. Так, например, с помощью комплексных чисел Гаусс нашел ответ на чисто геометрический вопрос: при каких натуральных n циркулем и линейкой можно построить правильный n-угольник? Из школьного курса геометрии известно, как циркулем и линейкой построить некоторые правильные многоугольники: правильный треугольник, квадрат, правильный шестиугольник (его сторона равна радиусу описанной около него окружности). Более сложным является построение правильных пятиугольника и пятнадцатиугольника. Научившись строить эти правильные многоугольники, легко перейти к построению соответствующих многоугольников с удвоенным числом сторон: восьмиугольника, десятиугольника и т. п. Все эти задачи на построение были решены еще в Древней Греции. Однако, несмотря на огромные усилия многих замечательных древнегреческих геометров и других ученых, никому не удалось построить ни правильный семиугольник, ни правильный девятиугольник. Не удалось также осуществить построение правильного р-угольника ни при каком простом числе р, кроме p = 3 и p = 5. Более двух тысяч лет никто не мог продвинуться в решении этой проблемы. В 1796 г. Карл Фридрих Гаусс, 19-летний студент-математик Геттингенского университета, впервые доказал возможность построения правильного семнадцатиугольника с помощью циркуля и линейки. Это было одно из самых удивительных открытий в истории математики. В течение нескольких последующих лет Гаусс полностью решил проблему построения правильных n-угольников.

Гаусс доказал, что правильный N–угольник с нечетным числом сторон (вершин) может быть построен с помощью циркуля и линейки тогда и только тогда, когда число N является простым числом Ферма или произведением нескольких различных простых чисел Ферма. (Числами Ферма называют числа вида F_n = + 1 · Приn = 0, 1, 2, 3, 4 эти числа являются простыми, при n = 5 число F₅ будет составным. Из этого результата следовало, что построение правильного многоугольника невозможно при N = 7, 9, 11, 13.

Легко заметить, что задача о построении правильного n-угольника равносильна задаче о делении окружности радиуса R = 1 на n равных частей. Выше было показано, что корень n-й степени из единицы имеет точно n значений; почти все эти значения (за исключением одного, двух) являются комплексными. Точки, изображающие корни n-й степени из единицы, располагаются на окружности радиуса R = 1 и делят ее на n равных дуг, т. е. являются вершинами правильного n-угольника, вписанного в эту окружность (см. рис. 3). При доказательстве возможности построения правильного 17-угольника Гаусс пользовался свойствами корней 17-й степени из единицы.

В XVIII в. возникла новая область математики – теория функций комплексной переменной. Введем понятие такой функции. Рассмотрим две комплексные переменные z = x + iy и w = u + iv, где x, y, u, v – действительные переменные, i = — мнимая единица. Зафиксируем две комплексные плоскостиOxy (плоскость z), O’uv (плоскость w) с выбранными на них системами прямоугольных координат и два множества на этих плоскостях: D и D’ соответственно (рис. 4).

Если каждой точке zD по некоторому закону f ставится в соответствие единственная точка wD’, то говорят, что w есть функция от z и пишут: w = f(z). Множество D в этом случае называют областью определения функции w = f(z), значения которой принадлежат области D’. Если множество значений f(z) исчерпывает все множество D’, то D’ называют множеством значений (областью изменения) функции f(z). B таком случае пишут: D’= f(D). Множества D и D’ можно изображать на одной комплексной плоскости. Каждое из множеств D и D’ может совпадать со всей плоскостью.

Таким образом, каждая комплексная функция реализует однозначное в одну сторону отображение одного множества на другое. Благодаря этому комплексные функции находят важные применения таких науках, как гидродинамика и аэродинамика, поскольку с их помощью удобно описывать движение объема жидкости (или газа).

С помощью теории функций комплексной переменной доказана следующая важная теорема, которую долгое время называли основной теоремой алгебры.

Теорема: Всякий многочлен с любыми числовыми коэффициентами, степень которого не меньше единицы, имеет хотя бы один корень, в общем случае комплексный.

Рассмотрим многочлен степени n (n ≥ 1):

Корнем многочлена называют такое число с (в общем случае комплексное: с = a + bi), которое обращает данный многочлен в нуль:

Другими словами, теорема утверждает, что алгебраическое уравнение n-й степени (n ≥ 1)

имеет хотя бы один корень.

Замечание. Не всякое уравнение имеет корни, действительные или комплексные. Например, трансцендентное (неалгебраическое) уравнение а x = 0 (а > 0) не имеет никаких корней (ни действительных, ни комплексных).

Геометрическое преобразование, при котором величины углов между любыми двумя линиями, содержащимися в преобразуемой фигуре, не изменяются, называют конформным преобразованием или конформным отображением. (Под углом между двумя линиями, пересекающимися в некоторой точке, понимают угол между касательными к этим линиям, проведенными в этой точке.) Примерами конформных отображений могут служить сдвиг (параллельный перенос), гомотетия и поворот. Таким образом, можно сказать, что функция w = z + с осуществляет конформное отображение; это одна из таких функций.

Теория функций комплексной переменной находит широкое применение при решении важных практических задач картографии, электротехники, теплопроводности и др. Во многих вопросах, где речь идет, например, об электрическом потенциале в точках пространства, окружающего заряженный конденсатор, или о температуре внутри нагретого тела, о скоростях частиц жидкости или газа в потоке, движущемся в некотором канале и обтекающем при этом некоторые препятствия, и т. п., нужно уметь находить потенциал, температуру, скорости и т. п. Задачи такого рода могут быть решены без особых затруднений в случае, когда встречающиеся в них тела имеют простую форму (например, в виде плоских пластин или круговых цилиндров). Однако расчеты необходимо уметь производить и во многих других случаях. Например, чтобы сконструировать самолет, надо уметь вычислять скорости частиц в потоке, обтекающем крыло самолета. Разумеется, при полете самолета движутся и частицы воздуха, и само крыло. Однако, опираясь на законы механики, исследование можно свести к случаю, когда крыло неподвижно, а на него набегает и обтекает его поток воздуха. Крыло самолета в поперечном разрезе, (профиль крыла) имеет вид, показанный на рисунке 7. Расчет скоростей производится достаточно просто, когда поперечный разрез обтекаемого тела есть круг (т. е. само тело является круглым цилиндром). Чтобы свести задачу о скоростях частиц потока воздуха, обтекающего крыло самолета, к более простой задаче обтекания круглого цилиндра, достаточно конформно отобразить часть плоскости, заштрихованную на рисунке 7, а (вне крыла), на другую фигуру, заштрихованную на рисунке 7, б (вне круга). Такое отображение осуществляется с помощью некоторой функции комплексной переменной. Знание этой функции позволяет перейти от скоростей в потоке, обтекающем круглый цилиндр, к скоростям в потоке, обтекающем крыло самолета, и тем самым полностью решить поставленную задачу.

Конформное отображение, заданное соответствующей функцией комплексной переменной, аналогичным образом позволяет сводить решение задач о расчете электрического потенциала и температур от случая тел произвольной формы (любого профиля сечения) к простейшим случаям, для которых задачи решается легко.

Список використаної літератури:

“Алгебра” С. Ленг Издательство МИР, Москва, 1968

“Кольца и модули” Ламбек, Иохаим. Издательство МИР, Москва, 1971

“Кольца(Элементы теории)”, Михалевич Ш. Х. Издательство Даугавпилоского педагогического института, 1973

“Алгебра: кольца, модулы и категории” Фейс К., Издательство МИР, 1977

“Кольца и модули. Предельные теоремы теории вероятности” Издательство ЛГУ, 1986

“Теория колец”, Джекобсон Н.. Государственное издательство иностранной литературы, Москва, 1947.

Источник