Применения теории графов в различных сферах
Научной деятельности
Изучая элементы теории графов, многие студенты задаются вопросом: «А где же собственно я могу применять графы?». Я попытаюсь привести примеры использования элементов теории графов в различных научных сферах и жизненных ситуациях.
Графы нашли применение практически во всех отраслях научных знаний: математике, физике, биологии, химии, истории, лингвистике, технике и т.п.
Самое распространенное применение теории графов нашла в математике при решении логических задач и головоломок. Основой применения графов для решения логических задач служит выявление и последовательное исключение возможностей, заданных в условии. Возьмем, к примеру, такую задачу: «На пришкольном участке растут 8 деревьев: яблоня, тополь, береза, рябина, дуб, клен, лиственница и сосна. Рябина выше лиственницы, яблоня выше клена, дуб ниже березы, но выше сосны, сосна выше рябины, береза ниже тополя, а лиственница выше яблони. Расположите деревья от самого низкого к самому высокому».
Теория графов в медицине. Каждому человеку важно знать свою группу крови и резус-фактор. Всего существует четыре группы крови. При переливании крови от одного человека к другому не все группы совместимы. Оказывается, с помощью графа можно наглядно показать возможные варианты переливания крови. Группы крови – это вершины графа с соответствующими номерами, а стрелки указывают на возможность переливания одной группы крови человеку с другой группой крови. Например, кровь первой группы можно переливать любому человеку, а человек с первой группой крови воспринимает только кровь своей группы. (рис.6)
Элементы теории графов используются и в экологии. Природные сообщества обладают сложным строением: несколькими уровнями, между которыми существуют разнообразные трофические (пищевые) и топические (не связные с цепью питания) связи. Структура трофической пирамиды может быть весьма различной, в зависимости от климата, почвы, ландшафта и других факторов.
При анализе биологических сообществ, принято строить пищевые или трофические сети, т.е. графы, вершины которых соответствуют видам, входящим в сообщество, а ребра указывают трофические связи между видами. Обычно такие графы – ориентированные: направление дуги между двумя вершинами указывает на тот из видов, который является потребителем другого, т.е. направление дуги совпадает с направлением потока вещества или биомассы в системе. Например трофическая сеть широколиственного леса. (рис.7)
Теория графов нашла своё применение и в архитектуре и строительстве. При составлении больших проектов, содержащих различные виды работ часто возникает ситуация, когда ту или иную работу можно начать лишь по окончании других. Так при строительстве дома нельзя приступить к отделочным работам, пока не возведены стены, и нельзя возводить стены до укладки фундамента. Последовательность работ изображается в виде сетевых графиков.
Графы в физике и технике. Одной из самых сложных и утомительных задач радиотехники было конструирование печатных схем.
Печатная схема – пластинка из изолирующего материала, на которой в виде металлических полосок вытравлены дорожки. Пересекаться дорожки могут только в определенных точках, куда устанавливаются необходимые элементы (диоды, триоды, резисторы и другие), их пересечение в других местах вызовет замыкание электрической цепи. Решение этой задачи упростилось благодаря использованию теории графов. В ходе решения этой задачи необходимо вычертить плоский граф, с вершинами в указанных точках. А благодаря теории графов эта задача теперь формализована, и расчёт дорожек производит компьютер. (рис.8)
Теория графов находит широкое применение в транспортных, коммуникационных системах. При строительстве новых кварталов, домов их принимают за вершины графа, а коммуникации – дороги, линии электропередачи, водопровод, тепловые сети – это рёбра и дуги.
Применение специальных методов на таком графе позволяет найти кратчайший удобный и оптимальный маршрут. При помощи графа производится поиск оптимальных путей прокладки коммуникаций. (рис. 9) В частности, графы широко применяются для маршрутизации данных в Интернете.
Помимо приведённых мной отраслей, в которых применяются графы, существует множество других.
Графы применяются в экономике и менеджменте, в информатике, в географии, в живописи, в психологии и рекламе. А также во многих других сферах нашей жизни.
Но всё-таки, существует ли такая область человеческих занятий, в которой теория графов, графы не играют никакой роли? Например, есть ли графы в искусстве, в музыке, поэзии?
Дата добавления: 2018-04-15 ; просмотров: 1916 ;
Применение графов в строительстве
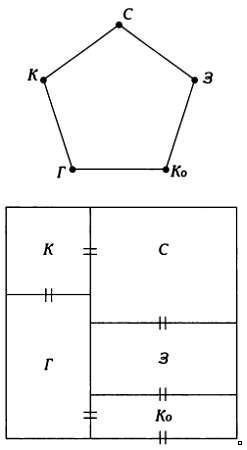
На первом этаже дома на одну семью (дом имеет прямоугольную форму) нужно расположить следующие элементы: кухню (К), столовую (С), зал, или жилую комнату (3), коридор (Ко) и гараж для автомобиля (Г). Между этими помещениями должны существовать проходы из гаража в кухню, из кухни в столовую, из столовой в зал, из зала в коридор и из коридора в гараж.
Если обозначить точками элементы К, С, 3, Ко и Г и соединить некоторые точки ребрами, обозначающими отношение «доступ к», получится граф, в котором четко виден цикл: при таком расположении комнат можно провести путь из любой комнаты в любую. На основе этого графа можно сделать различные эскизы.
Точками также можно обозначить наружное пространство или лестницу. Если речь идет о многоэтажных домах, то каждому этажу можно поставить в соответствие граф смежности и соединить точки, доступные с разных этажей, не прямыми, а ломаными линиями, которые будут обозначать лестницы.
Анализ графов в общественных зданиях поможет определить степень доступности различных отделов, расположение помещений — буфета, библиотеки, кинозала, а также пожарных лестниц.
После того как построен граф смежности и нарисован эскиз с нанесенными размерами, эскиз можно сопоставить с графом, где оцениваются размеры помещений согласно критерию, который объясняется ниже.
Обратите внимание, что все наши примеры очень просты. Графы особенно интересны при рассмотрении сложных ситуаций: в этом случае они позволяют существенно упростить анализ.
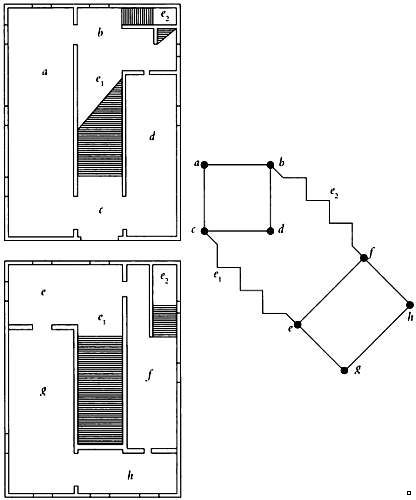
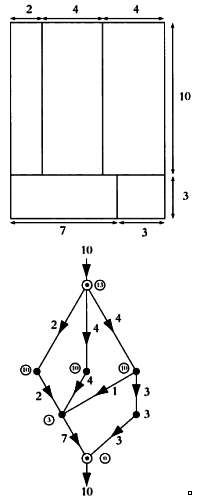
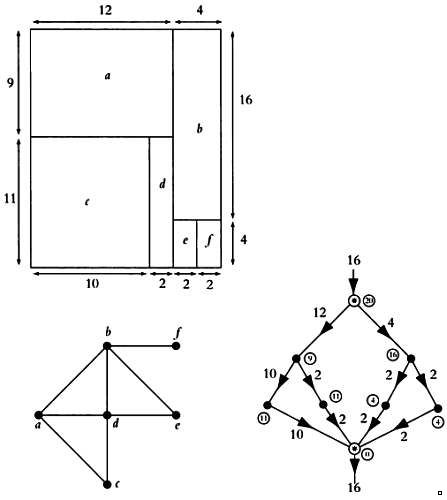
Нужно отметить вершины по числу стен, расположенных на чертеже горизонтально, а также две особые вершины — начальную и конечную. Все дуги графа должны быть направлены сверху вниз. Из каждой вершины выходят дуги, направленные вниз, на которых указываются размеры стен, расположенных на чертеже горизонтально.
На каждой вершине внутри круга указывается расстояние между стеной, соответствующей этой вершине, и следующей стеной, расположенной на чертеже горизонтально. В начальной вершине, точнее на входящем ребре, указывается общая ширина помещений, а внутри круга — их общая длина. В конечной вершине длина должна быть равна нулю, а на исходящем ребре должна быть нанесена общая ширина помещений. Заметим, что граф будет составлен неверно, если сумма значений для ребер, исходящих из данной вершины, будет не равна сумме значений для входящих ребер. Такие графы позволяют проверить правильность внутренних размеров помещений.
Еще один пример графов смежности представлен на следующих иллюстрациях.
Интерес в архитектуре также представляют графы, позволяющие оценить оптимальное расстояние между сообщающимися элементами. Это направление, особый вклад в развитие которого внес Т. Тейбор, описывает в общем виде оптимальное распределение архитектурных элементов, позволяющее сократить пути их обхода.
В небольшом масштабе эта задача не представляет интереса, но в ситуации, когда, например, на одном этаже офисного здания требуется разместить помещения, принадлежащие банку, министерству, администрации города и другим структурам, с помощью анализа стандартных маршрутов можно найти оптимальное расположение помещений, которое поможет упростить взаимодействия между организациями. Например, офисы одинаковой площади можно расположить на этаже в соответствии с одной из следующих пяти схем и эквивалентных им графов смежности.
Изучив расстояния между офисами (здесь мы имеем в виду реальное расстояние, которое нужно пройти, а не евклидово), можно определить, при каком из пяти расположений суммарный путь, который проходят сотрудники всех офисов, минимален. В экспериментах Тейбора использовалась скорость 1,5 м/с при перемещении по этажу и 0,3 м/с при перемещении по лестницам. Подобный принцип используется в урбанистике при проектировании крупных торговых центров и пешеходных зон, регулировании плотности транспортных потоков и для решения других подобных задач.
В теории графов применительно к архитектуре остается открытым вопрос о разбиении квадрата на прямоугольники горизонтальными и вертикальными линиями и определении всех возможных разбиений для каждого конкретного случая. Отметим, что цель задачи — найти не все возможные конечные графы, а только те, которые соответствуют допустимым разбиениям на плоскости.
Обозначим за n число прямоугольников, на которые мы хотим разбить квадрат. Было подсчитано, что для n = 1, 2, 3, 4, 5 и 6 существует соответственно 1, 1, 2, 7, 22 и 117 различных способов разбиения, которые не являются топологически эквивалентными.
Для n >= 7 эта задача до сих пор не решена. По некоторым оценкам,
для n = 7 существует около 700 решений, для n = 8 — примерно 10000, для n = 9 — порядка 250000 решений, но корректность подобной экстраполяции пока не подтверждена). Сегодня ученые занимаются поиском компьютерных алгоритмов решения этой задачи.
Индивидуальный учебный проект по теме «Графы и их применение»
Скачать:
Предварительный просмотр:
Муниципальное общеобразовательное учреждение
«Дашковская средняя общеобразовательная школа»
по теме: « Графы и их применение»
Пирогова Анастасия Юрьевна
Максимова Елена Леонидовна
Введение
Если вы любите решать задачи на смекалку или головоломки, то, наверное, составляли таблицы, изображали объекты точками, соединяли их отрезками или стрелками, выполняли над точками и отрезками операции, не похожие на арифметические, алгебраические или геометрические преобразования, то есть вам приходилось строить математический аппарат специально для решения задачи. А это означает, что вы заново открывали для себя начала теории графов.
Толчок к развитию теория графов получила на рубеже XIX и XX столетий, когда наибольший интерес стали вызывать работы по комбинаторике. Как отдельная математическая дисциплина теория графов была впервые представлена в работе венгерского математика Кёнига в 30-е годы XX столетия.
В настоящее время графы и связанные с ними методы исследований распространены практически на всю современную математику. Графы эффективно используются в теории планирования и управления, социологии, математической лингвистике, экономике, биологии, медицине. Широкое применение находят графы в таких областях прикладной математики, как в программирование, в решение вероятностных и комбинаторных задач.
ЦЕЛИ, ЗАДАЧИ И МЕТОДЫ ИССЛЕДОВАНИЯ
Цель исследовательской работы:
овладеть основными понятиями теории графов, новыми для школы методами решения задач, в популярной форме познакомиться с некоторыми приложениями теории графов для решения различных видов задач.
В этом проекте поставлены следующие задачи:
• Изучить элементы теории графов.
• Разобрать решения различных видов задач.
• Узнать о применении графов в науке и в различных сферах.
Методы исследования, которые используются в проекте:
Поиск и анализ информации в литературе и интернет – ресурсах.
I. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Графом в математике называется конечная совокупность точек, именуемых вершинами; некоторые из них соединены друг с другом линиями, называемых ребрами графа.
Инженер чертит схемы электрических цепей. Химик рисует структурные формулы, чтобы показать, как в сложной молекуле с помощью валентных связей соединяются друг с другом атомы. Историк прослеживает родословные связи по генеалогическому дереву. Военачальник наносит на карту сеть коммуникаций, по которым из тыла к передовым частям доставляется подкрепление. Социолог на сложнейшей диаграмме показывает, как подчиняются друг другу различные отделы одной огромной корпорации.
Что общего во всех этих примерах? В каждом из них фигурирует схема, состоящая из точек (они обозначают разветвления электрической цепи, атомы, людей, города и т.д.), соединённых между собой линиями.
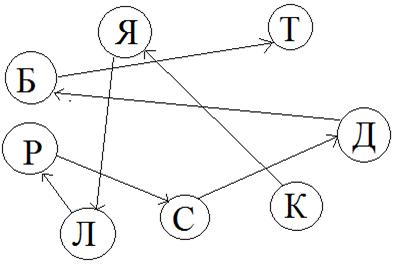
Задача 1. Между девятью планетами солнечной системы установлено космическое сообщение. Рейсовые ракеты летают по следующим маршрутам: Земля – Меркурий; Плутон – Венера; Земля – Плутон; Плутон – Меркурий; Меркурий – Вене; Уран – Нептун; Нептун – Сатурн; Сатурн – Юпитер; Юпитер – Марс и Марс – Уран. Можно ли долететь на рейсовых ракетах с Земли до Марса?
Решение: Нарисуем схему условия: планеты изобразим точками, а маршруты ракет – линиями.
Теперь нам видно, что долететь с Земли до Марса на рейсовых ракетах нельзя.
Задача 2. В одном городе шесть станций метро: Алмазная, Золотая, Лесная, Парковая, Садовая, Серебряная. Поезда следуют по маршрутам Алмазная – Золотая, Золотая – Серебряная, Серебряная – Алмазная. Лесная – Садовая, Садовая – Парковая, Парковая – Лесная. Можно ли с помощью этих поездов добраться со станции Парковая до станции Алмазная?
Решение: Нарисуем картинку, на которой будем отмечать станции точками, а соединяющие их маршруты – непересекающимися линиями.
Ответ: добраться со станции Парковая до станции Алмазная нельзя.
Граф для одной и той же задачи можно нарисовать разными способами; и наоборот для разных задач можно нарисовать одинаковые по виду графы. Здесь важно лишь то, какие вершины соединены друг с другом, а какие – нет. Например, граф для задачи 1 можно нарисовать по-другому:
Такие одинаковые, но по-разному нарисованные графы, называются изоморфными
Что общего у схем, которые помогли решить нам задачи? Все они состоят из точек (кружков) и отрезков, соединяющих пары точек. Рассмотрение таких схем и приводит к понятию графа.
Обозначать граф будем буквой Г. При изображении графов на рисунках или схемах отрезки могут быть прямолинейными и криволинейными; длины отрезков и расположение точек произвольны.
Все три фигуры на рисунке изображает один и тот же граф.
3. Взвешенный граф – дуги или ребра имеют вес.
Две вершины А и В графа называются связными, если в графе существует путь с концами А и В.
Две вершины графа называются несвязными, если в графе не существует ни одного пути, связывающего их.
Про граф, изображенный на рисунке, говорят, что он связный, так как из каждой вершины по ребрам можно попасть в любую другую.
Несвязный граф имеет вид нескольких “кусков”, каждый из которых – либо отдельная вершина без ребер, либо связный граф.
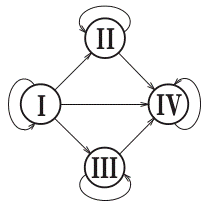
Граф называется полным, если каждые две различные вершины его соединены одним и только одним и только одним ребром.
В полном графе каждая его вершина принадлежит одному и тому же числу
ребер. Для задания полного графа достаточно знать число его вершин.
Граф, не являющийся полным, можно преобразовать в полный с теми же вершинами, добавив недостающие ребра. Например, граф на рисунке 11 неполный. Проведя недостающие ребра (для удобства их можно выделить другим цветом или другим типом линии), получаем полный граф с пятью вершинами (рис. 12).
1.4. Степень вершины
Степенью вершины называется число ребер графа, которым принадлежит эта вершина.
У графа на рисунке 13 (а): степень= 1; на рисунке 13(б) степень = 2. У графа на рисунке 13 (в) степени всех вершин равны нулю.
Имея даже общие представления о графе, иногда можно судить о степенях его вершин. Так, степень каждой вершины полного графа на единицу меньше числа его вершин. При этом некоторые закономерности, связанные со степенями вершин, присущи не только полным графам.
1.5. Свойства графов:
1. Если все вершины графа четные, то можно одним росчерком (т.е. не отрывая карандаша от бумаги и не проводя дважды по одной и той же линии) начертить граф. При этом движение можно начать с любой вершины и окончить в той же вершине.
3. Граф с более чем двумя нечетными вершинами невозможно начертить одним росчерком.
4. Число нечетных вершин графа всегда четное.
Доказательство : Количество ребер графа равно половине суммы степеней его вершин. Так как количество ребер должно быть целым числом, то сумма степеней вершин должна быть четной. А это возможно только в том случае, если граф содержит четное число нечетных вершин.
5. Если в графе имеются нечетные вершины, то наименьшее число росчерков, которыми можно нарисовать граф будет равно половине числа нечетных вершин этого графа.
II. ИССЛЕДОВАТЕЛЬСКАЯ ЧАСТЬ
2.1. Применение графов к решению задач по математике.
Задача 1. Девять шахматистов проводят турнир в один круг (каждый из участников должен сыграть с каждым из остальных по одному разу). Докажите, что в любой момент найдутся двое, закончившие одинаковое число партий.
Задача 2. В городе Маленьком 15 телефонов. Можно ли их соединить проводами так, чтобы каждый телефон был соединен ровно с пятью другими?
Задача 3. Охотник за мертвыми душами Павел Иванович Чичиков побывал у помещиков по одному разу у каждого. Он посещал их в следующем порядке: Манилова, Коробочку, Ноздрева, Собакевича, Плюшкина, Тентентникова, генерала Бетрищева, Петуха, Констанжогло, полковника Кошкарева. Найдена схема, на которой Чичиков разбросал взаимное расположение имений и проселочных дорог, соединяющих их. Установите, какое имение кому принадлежит, если ни по одной дороге Чичиков не проезжал более одного раза.
Решение. По схеме видно, что путешествие Чичиков начал с имения Е, а закончил имением О. В имения В и С ведут только две дороги, поэтому по ним Чичиков должен был проехать.
2.2. Применение графов в решении практических задач из разных областей деятельности.
2.2.1. Графы в структуре управления
— Уровень государственно – общественного управления
Эту связь мы можем увидеть с помощью графов.
2.2.2. Графы в психологии.
В каждой школе имеется школьный психолог, который изучает взаимоотношения между учениками в классе. Чтобы представить более детально и наглядно картину отношений в группе (классе), можно построить специальные диаграммы, называемые социограммами. Это выполненные по определенной схеме рисунки, на которых при помощи соответствующих условных обозначений отмечаются все выявленные в исследованной группе выборы и отклонения. Чаще строятся так называемые социограммы – мишени.
Число концентрических окружностей, из которых состоит социограмма – мишень, обычно соответствует максимальному количеству выборов, полученных в данной группе кем-либо из её членов. Лидер в группе условно показан на социограмме в центре. Остальные участники группы располагаются на социограмме – мишени на периферии в пределах тех окружностей, которые соответствуют числу полученных ими выборов. От центра к периферии это число уменьшается. Наконец, за пределами всех окружностей, имеющихся на социограмме – мишени, располагаются те члены, которых не выбрал никто. Это – изолированные от остальных участники группы, не имеющие положительных взаимоотношений с другими членами.
Представляемые на социограммах данные нередко для получения более подробной информации о положении человека в системе внутригрупповых отношений дополняются числовыми показателями – индексами. Наиболее известный из них индекс групповой сплоченности, который характеризует систему новых отношений в целом. Изучив данный материал, я применила всё на практике и результаты исследуемых вывела на этой социограмме. Я провела опрос в своем классе. Мои одноклассники отвечали на вопрос: «С кем бы вы хотели сидеть?» Лидер определяется по количеству выборов.
Выполняя данный проект, я овладела основными понятиями теории графов, узнала новые для школы методы решения математических задач, изучила элементы теории графов, узнала о применении графов в науке и различных сферах жизнедеятельности. Я сделала вывод, что графы во многом облегчают нашу жизнь. Это относится не только о их применении в школе, но и в реальной жизни.